Сегодня я расскажу о числах в python, а также о их операциях. В Python существует 4 вида чисел:
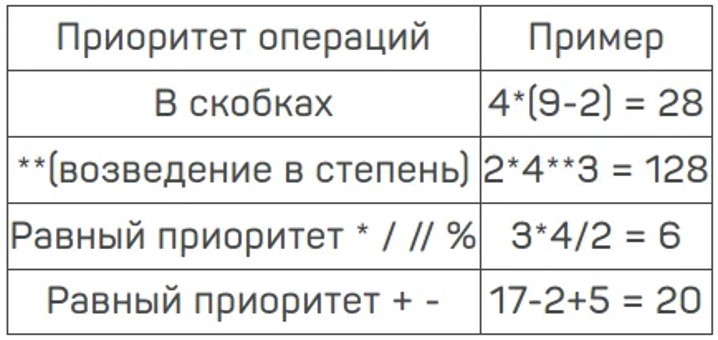
Приоритет выполнения операций:
- Целые числа (int)
- Вещественные числа (float)
- Комплексные числа (complex)
- Десятичные дроби (decimal)
Приоритет выполнения операций:
Целые числа (int)
Целые числа в Python ничем не отличаются от обычных чисел. Они поддерживают набор самых обычных математических операций:

Битовые операции
Над целыми числами также можно производить битовые операции.

Методы
int.bit_length() — количество бит, необходимых для представления числа в двоичном виде, без учёта знака и лидирующих нулей. Пример:
n = -37
bin(n)
# Выведет: '-0b100101'
n.bit_length()
# Выведет: 6int.to_bytes(length, byteorder, *, signed=False) — возвращает строку байтов, представляющих это число. Пример:
(1024).to_bytes(2, byteorder='big')
# Выведет: b'\x04\x00'
(1024).to_bytes(10, byteorder='big')
# Выведет: b'\x00\x00\x00\x00\x00\x00\x00\x00\x04\x00'
(-1024).to_bytes(10, byteorder='big', signed=True)
# Выведет: b'\xff\xff\xff\xff\xff\xff\xff\xff\xfc\x00'
x = 1000
x.to_bytes((x.bit_length() // 8) + 1, byteorder='little')
# Выведет: b'\xe8\x03'classmethod int.from_bytes(bytes, byteorder, *, signed=False) — возвращает число из данной строки байтов. Пример:
int.from_bytes(b'\x00\x10', byteorder='big')
# Выведет: 16
int.from_bytes(b'\x00\x10', byteorder='little')
# Выведет: 4096
int.from_bytes(b'\xfc\x00', byteorder='big', signed=True)
# Выведет: -1024
int.from_bytes(b'\xfc\x00', byteorder='big', signed=False)
# Выведет: 64512
int.from_bytes([255, 0, 0], byteorder='big')
# Выведет: 16711680Вещественные числа (float)
Вещественные числа поддерживают те же операции, что и целые. Но вещественные числа неточны, и это может привести к ошибкам:
0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1
# Выведет: 0.9999999999999999Вещественные числа не поддерживают длинную арифметику:
a = 3 ** 1000
a + 0.1
# Выведет: Traceback (most recent call last):
File "", line 1, in
OverflowError: int too large to convert to floatМетоды
- float.as_integer_ratio() — пара целых чисел, их отношение равно этому числу.
a = float.is_integer_ratio(4.0)
print (a)
Выведет: 4, 1- float.is_integer() — является ли значение целым числом.
a = float.is_integer(4.0)
print (a)
Выведет: True
a = float.is_integer(4.1)
print (a)
Выведет: False- float.hex() — переводит float в hex (шестнадцатеричную систему счисления).
a = float.hex(4.0)
print(a)
Выведет: 0x1.0000000000000p+2- float.fromhex(s) — float из шестнадцатеричной строки.
a = float.fromhex("0x1.0000000000000p+2")
print(a)
Выведет: 4.0Также для работы с числами в Python есть несколько полезных модулей.
Модуль math предоставляет более сложные математические функции. Например:
Модуль math предоставляет более сложные математические функции. Например:
import math
math.pi
# Выведет: 3.141592653589793
math.sqrt(85)
# Выведет: 9.219544457292887Модуль random реализует генератор случайных чисел и функции случайного выбора. Например:
import random
random.random()
# Выведет: 0.15651968855132303
import random
a = random.randint(1,100)
print(a)Комплексные числа (complex)
Примеры работы комплексных чисел в Python:
x = complex(1, 2)
print(x)
# Выведет: (1+2j)
y = complex(3, 4)
print(y)
# Выведет: (3+4j)
z = x + y
print(x)
# Выведет: (1+2j)
print(z)
# Выведет: (4+6j)
z = x * y
print(z)
# Выведет: (-5+10j)
z = x / y
print(z)
# Выведет: (0.44+0.08j)
print(x.conjugate()) # Сопряжённое число
# Выведет: (1-2j)
print(x.imag) # Мнимая часть
# Выведет: 2.0
print(x.real) # Действительная часть
# Выведет: 1.0
print(x > y) # Комплексные числа нельзя сравнить
# Выведет: Traceback (most recent call last):
File "", line 1, in
TypeError: unorderable types: complex() > complex()
print(x == y) # Но можно проверить на равенство
# Выведет: False
abs(3 + 4j) # Модуль комплексного числа
# Выведет: 5.0
pow(3 + 4j, 2) # Возведение в степень
# Выведет: (-7+24j)Также в Python существует интересный модуль под назанием cmath. Данный модуль предоставляет функции для работы с комплексными числами:
- cmath.phase(x) — возвращает фазу комплексного числа
- cmath.polar(x) — преобразование к полярным координатам. Возвращает пару (r, phi).
- cmath.rect(r, phi) — преобразование из полярных координат.
- cmath.exp(x) — ex.
- cmath.log(x[, base]) — логарифм x по основанию base. Если base не указан, возвращается натуральный логарифм.
- cmath.log10(x) — десятичный логарифм.
- cmath.sqrt(x) — квадратный корень из x.
- cmath.acos(x) — арккосинус x.
- cmath.asin(x) — арксинус x.
- cmath.atan(x) — арктангенс x.
- cmath.cos(x) — косинус x.
- cmath.sin(x) — синус x.
- cmath.tan(x) — тангенс x.
- cmath.acosh(x) — гиперболический арккосинус x.
- cmath.asinh(x) — гиперболический арксинус x.
- cmath.atanh(x) — гиперболический арктангенс x.
- cmath.cosh(x) — гиперболический косинус x.
- cmath.sinh(x) — гиперболический синус x.
- cmath.tanh(x) — гиперболический тангенс x.
- cmath.isfinite(x) — True, если действительная и мнимая части конечны.
- cmath.isinf(x) — True, если либо действительная, либо мнимая часть бесконечна.
- cmath.isnan(x) — True, если либо действительная, либо мнимая часть NaN.
- cmath.pi — π.
- cmath.e — e.
Десятичные дроби
Числа данного типа позволяют производить вычисления над десятичными дробями с заданной точностью. Примеры:
from decimal import *
getcontext().prec = 10 # число знаков после запятой
a = Decimal(13) / Decimal(17)
print(a) # выведет: 0.7647058824# квадратный корень из 3
from decimal import *
getcontext().prec = 10
a = Decimal(3).sqrt()
print(a)
input()# корень 7-й степени
from decimal import *
getcontext().prec = 10
a = Decimal(3)**Decimal(1/7)
print(a)
input()# натуральный логарифм
from decimal import *
getcontext().prec = 10
a = Decimal(3).ln()
print(a)
input()Видео по уроку: